Docsity
Log inSign up
Docsity
Prepare for your exams
Prepare for your exams

Study with the several resources on Docsity

Earn points to download
Earn points to download

Earn points by helping other students or get them with a premium plan

Guidelines and tips
Guidelines and tips
Sell on Docsity
Sell on Docsity
Log inSign up

Prepare for your exams

Study with the several resources on Docsity

Find documents

Prepare for your exams with the study notes shared by other students like you on Docsity

Search Store documents

The best documents sold by students who completed their studies

Search through all study resources
Docsity AINEW

Summarize your documents, ask them questions, convert them into quizzes and concept maps

Explore questions

Clear up your doubts by reading the answers to questions asked by your fellow students

Earn points to download

Earn points by helping other students or get them with a premium plan

Share documents
download point icon20 Points

For each uploaded document

Answer questions
download point icon5 Points

For each given answer (max 1 per day)

All the ways to get free points
Get points immediately

Choose a premium plan with all the points you need

Study Opportunities

Choose your next study program

Get in touch with the best universities in the world. Search through thousands of universities and official partners

Community

Ask the community

Ask the community for help and clear up your study doubts

University Rankings

Discover the best universities in your country according to Docsity users

Free resources

Our save-the-student-ebooks!

Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors

From our blog

Exams and Study
Go to the blog

Engineering Dynamics Practice Problems for Finals: ENGR 2090, Fall 2023, Exams of Mechanical Engineering

Rensselaer Polytechnic Institute (RPI)Mechanical Engineering

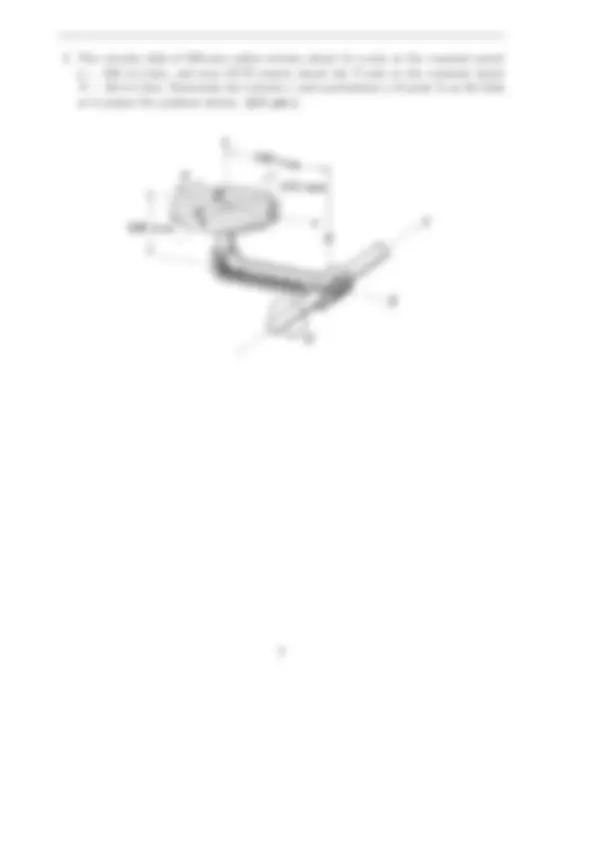
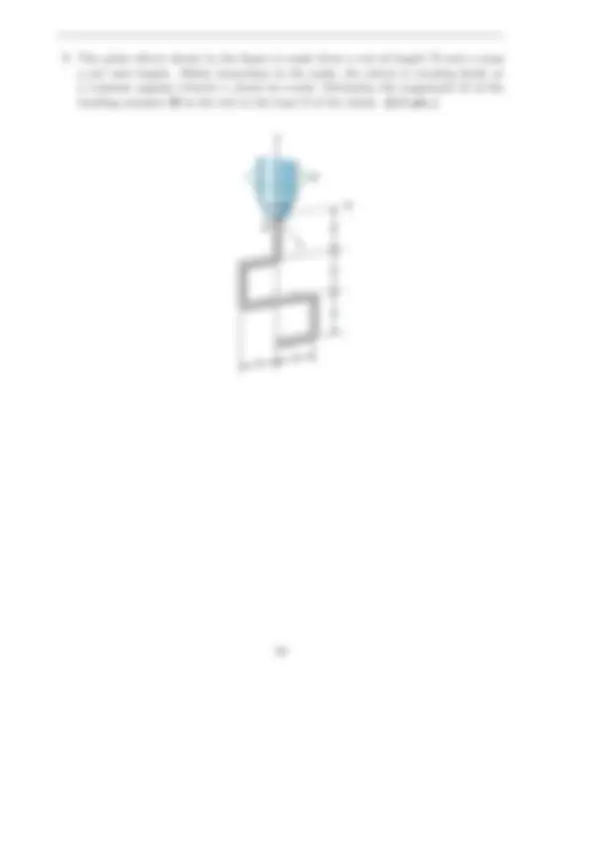
A set of practice problems for the final exam in engr 2090: engineering dynamics at rensselaer polytechnic institute. The problems cover the last third of the course, focusing on topics such as rotational motion, angular momentum, and gyroscopic effects. Designed to help students prepare for the final exam by providing them with a comprehensive set of practice problems that cover the key concepts and principles of the course.

Typology: Exams

2022/2023

Uploaded on 02/05/2025

hanlin-wang
hanlin-wang 🇺🇸

6 documents

1 / 10

Toggle sidebar

This page cannot be seen from the preview

Don't miss anything!

bg1
Rennselaer Polytechnic Institute
School of Engineering
ENGR 2090: Engineering Dynamics
HW 10/Practice Problem Set - Finals
Section 04, Instructor: Professor Singh
Due: Dec. 8, 2023 at 23:59:00 EDT Semester: Fall 2023 Max points: NA
Note the following:
•This practice set is based on the last third of the course.
•You can expect 2/3 problems on the exam from the last third of the course.
•Remember that one problem on the exam will be from the first two-thirds of the
course.
•Please review the HW Problems, Example Problems and ICAs along with this
problem set to be best prepared.
1
pf3
pf4
pf5
pf8
pf9
pfa

Partial preview of the text

Download Engineering Dynamics Practice Problems for Finals: ENGR 2090, Fall 2023 and more Exams Mechanical Engineering in PDF only on Docsity!

Rennselaer Polytechnic Institute

School of Engineering

ENGR 2090: Engineering Dynamics

HW 10/Practice Problem Set - Finals

Section 04, Instructor: Professor Singh

Due: Dec. 8, 2023 at 23:59:00 EDT Semester: Fall 2023 Max points: NA

Note the following:

  • This practice set is based on the last third of the course.
  • You can expect 2/3 problems on the exam from the last third of the course.
  • Remember that one problem on the exam will be from the first two-thirds of the course.
  • Please review the HW Problems, Example Problems and ICAs along with this problem set to be best prepared.
  1. The design of the rotating arm OA of a control mechanism requires that it ro- tate about the vertical Z-axis at the constant rate Ω = β˙ = 3. rad/s. Simultaneously, OA oscillates according to θ = θ 0 sin (4Ωt), where θ 0 = 0.523598775598299 radians and t is in seconds measured from the time when β = 0. Determine the velocity vA and acceleration aA of the ball tip A for the condition when t = 0.5 s. Distance b = 120 mm, s = 100 mm, Ω = 3.14159265358979 rad/s. (2.5 pts.)
  1. The thin circular disk of radius r = 100 mm is rotating about its z−axis with a constant angular velocity p = 40 rad/s, and the yoke in which it is mounted rotates about the x−axis through OB with a constant angular velocity ω 1 = 3 rad/s. Simultaneously, the entire assembly rotates about the fixed Y −axis through O with a constant angular velocity ω 2 = 2 rad/s. Determine the kinetic energy T and the angular momentum HO with respect to O of the disk for the instant represented, when the x-y plane coincides with the X-Y plane. The mass of the disk is m = 2 kg and the distance b is 200 mm. (2.5 pts.)
  1. The uniform slender bar of mass m and length l is centrally mounted on the shaft A-A, about which it rotates with a constant speed ϕ˙ = p. Simultaneously, the yoke is forced to rotate about the x−axis with a constant speed ω 0. Determine the magnitude of the torque M required to maintain the constant speed. Ignore the mass of the yoke. Use the values m = 5 kg, l = 300 mm, p = 18 rad/s, ω 0 = 5 rad/s, and ϕ˙ = 30°. (2.5 pts.)
  1. The housing of the electric motor is freely pivoted about the horizontal x-axis, which passes through the mass center G of the rotor. If the motor is turning at the constant rate ϕ˙ = p, determine the angular acceleration, ψ¨ which will result from the application of the moment M about the vertical shaft if ˙γ = ψ˙ = 0. The mass of the frame and housing is considered to be negligible compared to the mass m of the rotor. The radius of gyration of the rotor about the z-axis is kz and that about the x-axis is kx. (2.5 pts.)
  1. Each of the slender rods of length l and mass m is welded to the circular disk which rotates about the vertical z-axis with an angular velocity ω. Each rod makes an angle β with the vertical and lies in a plane parallel to the y − z plane. Determine an expression for the angular momentum HO of the two rods about the origin O of the axes. (2.5 pts.)
  1. The paint stirrer shown in the figure is made from a rod of length 7b and a mass ρ per unit length. Before immersion in the paint, the stirrer is rotating freely at a constant angular velocity ω about its z-axis. Determine the magnitude M of the bending moment M in the rod at the base O of the chuck. (2.5 pts.)