Download Mathematics Quiz 16 and more Quizzes Engineering Mathematics in PDF only on Docsity!
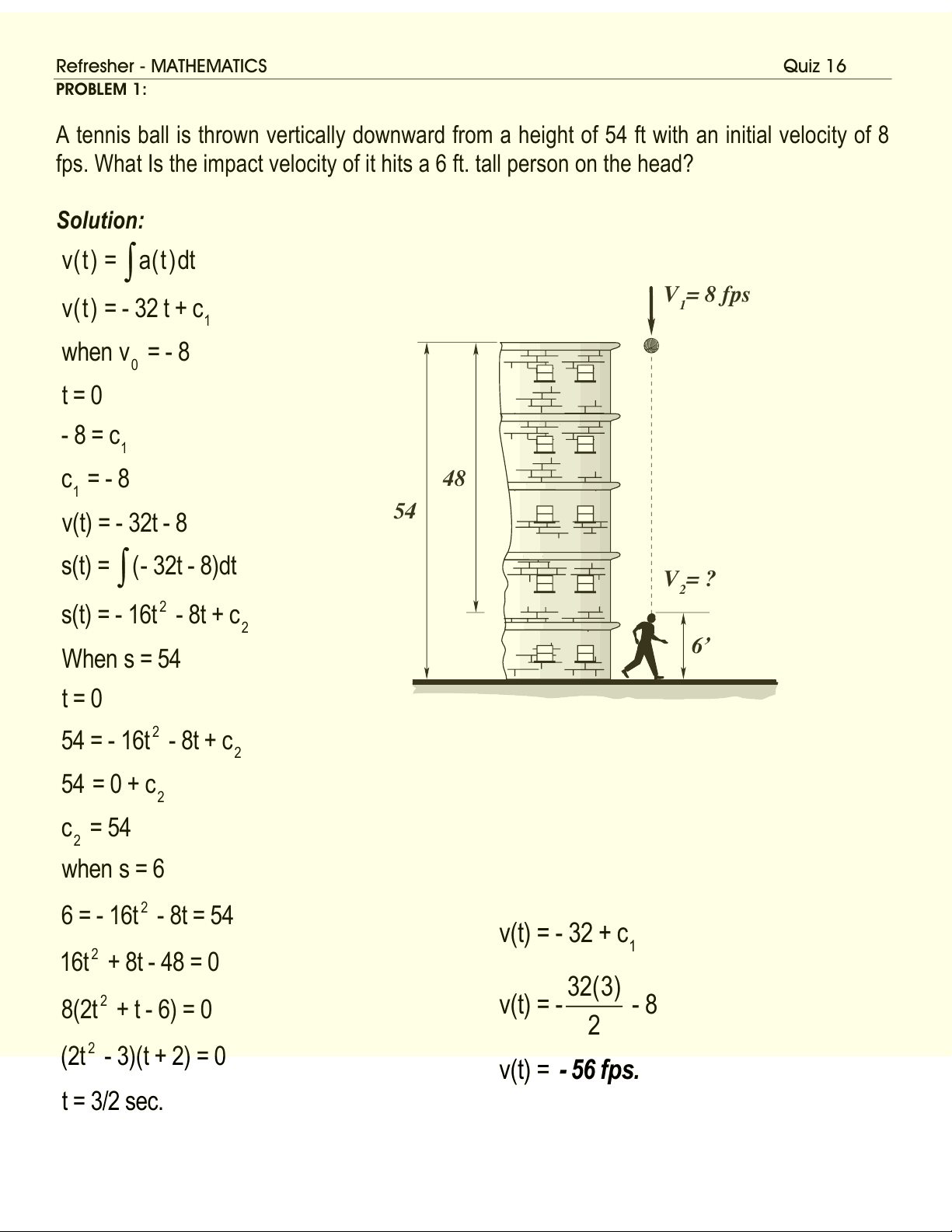
PROBLEM 1: A tennis ball is thrown vertically downward from a height of 54 ft with an initial velocity of 8 fps. What Is the impact velocity of it hits a 6 ft. tall person on the head? Solution: when s = 6 6 = - 16 t 2
- 8 t - 48 = 0 8 ( 2 t 2
- t - 6 ) = 0 ( 2 t 2
- 3 )(t + 2 ) = 0 t = 3 / 2 sec. v(t) = - 32 + c 1 v(t) = -
v(t) = - 56 fps. v(t) = a(t)dt
v(t) = - 32 t + c 1 when v 0 = - 8 t = 0
- 8 = c 1 c 1 = - 8 v(t) = - 32 t - 8 s(t) = (
- 32 t - 8 )dt s(t) = - 16 t 2
- 8 t + c 2 When s = 54 t = 0 54 = - 16 t 2
- 8 t + c 2 54 = 0 + c 2 c 2 = 54 54 48 V 1 = 8 fps V 2 =? 6’
PROBLEM 2 :
In triangle ABC, AB = 30 m., BC = 36 m. and AC = 48 m. has an area
equal to 539.32 m^2. How far is the point of intersection of the
perpendicular bisectors from A?
Solution:
A B C r^ r (^30) r 36 48 A = abc 4 r
- 32 = ( 36 )( 48 )( 30 ) 4 r r = 24. 03 m. from A
f(c) = 7 3
- 2 3 2 3 PROBLEM 4 : Find the height f(c) of rectangle so that the area A under the graph of y = x^2 + 1 on [-2, 2] is the same as f(c) = [2 - (- 2)] = 4 f(c). Solution: A = ydx
- 2 A = 28 3 4 f(c) = 4 (c 2
- 1 ) 4 (c 2
- 1 ) = 28 3 c 2
- 1 = 7 3 3 c 2
- 3 = 7 3 c 2 = 4 c= 2 3 f(c) = c 2
- 1 f(c) = 2 3 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2
- 1 f(c) = 4 3
- 1 f(c) = 7 3 -2 2 y = x^2 +
PROBLEM 5 :
Find the volume V of the solid formed by revolving the region bounded by
the graphs of , y = 0, and x = 4 about the x – axis.
Solution:
V = πy
2
dx
0 4
V = π x dx
0 4
V = π
x
2
0 4
V = 8 π
y = x
x y dx y y =√ x x = x = Area dx r = y
PROBLEM 7 :
Determine the nominal interest rate corresponding to an effective interest
rate of 10% per year, compounded continuously.
Solution:
Effective rate = er^ – 1
0.10 = e
r
er^ = 1.
r = 0.
r = 9.53%
PROBLEM 8 : An experiment consists of inspecting items from a production line until a defective (D) is found. Give the sample space for this experiment. Give the sample space for this experiment. S = {D, ND, NND, NNND…….} Which outcomes are in the events A, B and C , If at least 2 are inspected.
P a) {ND, NND, NNND…….}
b) {NNN, NND, DNN…….} c) {DDD, DNN, NDD…….} d) {NDD, DND, DDN…….}
PROBLEM 10 :
A quadrilateral ABCD is inscribed in a circle having a diameter AD =
8.224 cm. If AB = 2 cm, BC = 4 cm, and CD = 6 cm, find the area of the
quadrilateral.
Solution:
S = a + b + c + d 2 S = ( 2 + 4 + 6 + 8. 224 ) 2 S = 10. 112 A = (S - a)(S - b)(S - c)(S - d) A = 19. 6 cm 2 A (^) D C B a = b = d =8. c =
PROBLEM 11 :
Given the following partial fraction with its corresponding partial fraction.
What is the value of B?
Solution
x 2
x 2 (x 2
- 2 x + 2 ) 4 x
- B(x 2
- x + 2 ) + (x + 3 )x 2 4 x 2
- 2 x + 3 = x(x 2
- 2 x + 2 ) 4
- B(x 2
- 2 x + 2 ) + (x - 3 )x 2 4
when x = 0
0 + 0 + 3 = 0 + 2 B + 0
B = 1. 5
x
2
+ 2 x + 3
x
4
+ x
3
+ 2 x
2
4 x
B
x
2
x + 3
4 (x
2
+ x + 2 )
