Download Motors and Motion Control: Types, Characteristics, and Equations - Prof. Stephen L. Canfie and more Exams Mechanical Engineering in PDF only on Docsity!
Overview of motors and motion control
- Elements of a motion-control system
High-level controller
Low-level controller
Driver
Power Supply
Motor
- Types of motors discussed here;
Brushed, PM DC Motors
Stepper Motors Brushless DC Motors
Brushless AC Motors Cheap, rugged, high-reliability
Cheap, rugged, high-reliability
No brushes, suitable for any environment
No brushes, suitable for any environment Low Torque ripple No brushes, suitable for any environment Do not require feedback At low speeds, provide up to 5x torque of brushed motor, 2x torque of brushless motor Suffers from resonance and long settling times Consume current regardless of load or motion, run hot Losses at speed are high Undetected position loss as a result of open loop operation
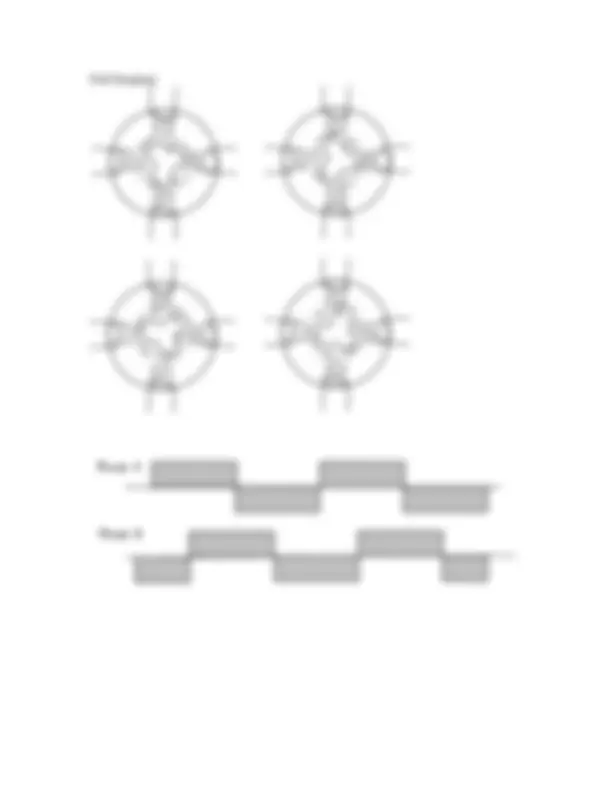
Stepper Motors
Half Stepping
N
S
N S
N
S N
N
S S
S N N
S N
N
S S
Phase A
Phase B
Stepper (cont.) Wiring arrangements for various Steppers
∼6Ω
4-lead (^) 5-lead (^) 6-lead 8-lead
Behavior of stepping-motor
- A typical step motor has 200 full step positions. Thus, the typical stepper will move 1.8 degrees in one step.
- When the stator portion of the stepper makes a step (but prior to the rotor actually moving), the stepper sees its maximum torque. As the rotor moves under the influence of this torque, the torque drops to a zero value when the rotor reaches the end of its step (1.8 degrees).
- This results in a static torque curve that may look something like:
(^0) 1.8 3.
degrees
Torque Max T.
Start step Stable
- Considering the static torque curve above, the rotor on a step motor could lag commanded motion by as much as 1.8 degrees during an acceleration phase, or lead by as much as 1.8 degrees during deceleration.
Note that the static torque curve of a stepper behaves similar to a mass-spring system with a non-linear spring. From this model, the response to a single step move would look something like;
angle
time
- Due to this behavior of the step motor, driving the motor at a step speed near its natural frequency can greatly increase the oscillations during response. The natural frequency of the motor depends on the stiffness (electro-magnetic field) and rotational inertia. Higher inertia will decrease the natural frequency of the system and provide more separation between typical driving frequencies and ωn. Typical ωn for an unloaded stepper may be 100-200 Hz.
- An additional consideration in driving steppers is the acceleration profile. Remember that the maximum torque of the system cannot be exceeded. Therefore, to operate at a desired rotation or slew rate, the motor must be started (and stopped) in a profiled manner, approaching the desired speed such that the motor is not driven past maximum acceleration.
Vin = Ldidt + Ri + ke ω,
a first order ODE in current, i, with L , R the motor inductance and resistance, ke the electric constant, Vemf the back emf and ω the rotational speed of the motor (rad/s).
Motor Mechanics:
The rotational inertia, J as seen by the motor is, 2
2
1 ⎟
g
g motor load d
d J J J ,
accounting for motor inertia (rotor) as well as gear train and load inertia. Motor Dynamics:
J θ&& + C θ&= T − Tfriction ,
This second order ODE in rotation, θ, with C viscous damping in the system, T the motor
torque and Tfriction the friction torque describes the motor dynamics.
Finally, the electro-mechanical relation is approximately given as an equation that describes motor torque as a linear function of current in the motor, T = kt i
where kt the motor torque constant.
These equations can be combined to result in two equations, a 1st^ and 2nd^ order ODE with two unknowns, i and q ;
J θ + C θ− kt i =− T friction
Li ′+ Ri + ke θ= V in
These will be cast in state-space form to result in a system of three 1st^ order DE’s’
x i
x
x
3
2
1
L
x V L x R L x k
x CJx k J x T
x x
b in
t friction
3 2 3
2 2 3
1 2
or;
Jload (^) g 2
Jmotor g 1
motor
T
θ, ω, α
3
2
1
3
2
1
3
2
1
3
2
1
x
x
x
y
y
y
V
L
x R
x
x
L
R
L
k
J
k J
C
x
x
x
b
t &
Matlab provides a variety of tools to easily model this system. A simple first step could be to observe a step response of this system (step input of the motor voltage) using the command;
step(A,V*B,C,D) with A,B,C the matrices shown above (in order).
Steady-State Motor Behavior:
At steady state, the dynamic motor model above can be greatly simplified ( i_dot , θ _dot =
- to yield the equations;
Ri + ke ω = V in + T = kti Æ
⎟^ ω
R
V k k k T R in e t t
,
This equation represents a linear torque/speed relation for a PM dc motor. The response (assuming a constant input applied voltage) looks like;
Torque
Power
T,P Tstall
ωno load
ω
The maximum generated torque occurs at rest (stall), and decreases to zero at the maximum motor speed under no load. At this speed, the back-emf voltage in the motor is equal to the input voltage (minus a small amount to overcome inefficiencies in the motor).
Problem givens; M=10kg; rw=8cm; g2:g1=GR=50; Jload = .0001 kgm^2 ; θ = 30deg., consider friction in the system as a percentage of the static load.
Analysis Approach; First we need to get our state equations. These will consist of equations of motion, our KVL equations and our electro-mechanical relations as derived above. The KVL relation will be identical to that above. Create a simple FBD of the motor system to get the equations of motion;
FBD:
Jequiv
Equations:
GR
T
GR
J (^) equiv C kti Mg friction
θ&& θ& sin θ
Li ′+ Ri + ke θ&= V in
Note that the variable q is the motor rotation. Jequiv. is the equivalent inertia of the system as seen by the motor and determined using the relation described above. Remember that inertia’s are magnified by the square of intermedi gear reductions. In this case, Jequiv. is given as;
2
2 2 1 1
payload w
equiv armature conveyor payload
J Mr
GR
J
GR
J J J
Equations in State-Space Form:
x i
x
x
3
2
1
T
θ, ω, α
Mgsin(θ)/g
3
2
1
3
2
1
3
2
1
3
2
1
sin
x
x
x
GR
r
GR
r
y
y
y
L
RV
J GR
T
J GR
Mg
x
x
x
L
R
L
k
J
k J
C
x
x
x
w
w
friction
b
t^ θ
Note that in describing that observers or outputs, y a conversion is made to output displacement and velocity in meters and m/s respectively, y 3 still represents current.
Solution approach: Implement using the step function in Matlab. In this case, the system will be described in state space form with the matrices A, B, C (D=[]) as above.
Example: Consider the SM233A motor from Parker automation (page 188 in ’99 computmotor catalog). The specifications on this motor are as follows; Jarmature = 1.3e-4 kg m^2 ; kt = .415 N.A; kb=50.6860/(2pi*1000) N m s; L= 4.8e-3 H, R = 9.65O, V=
Matlab code: M=10; %Payload mass g=9.81; %gravity Jconv=.0001; %Conveyor inertia rw=.08; %Wheel radius dg1=1;dg2=25;GR=dg2/dg1; J_motor=1.3e-4; %Motor inertia J=J_motor+Jconv(1/GR)^2+Mrw^2(1/GR)^2; %Total inertia at motor C=1.0791e-5; %Viscous damping theta=30pi/180; kt=.415; % torque constant kb=50.6860/(2pi1000); %Back emf constant L=4.81e-3; %Inductance R=9.65; %Resistance V=12; %Input voltage Tf=.5; %frictional torque as a percent of dead load A=[0,1, 0,-C/J,kt/J 0,-kb/L,-R/L]; B=[0;(-Mgrwsin(theta)/GR)(1+Tf)/J;V/L]; C=[rw/GR,0,0;0,rw/GR,0;0,0,1]; D=[0;0;0]; step(A,B,C,D)
Step R es pons e
Tim e (s ec)
Am plitude
0
From : U (1)
To: Y(1)
0
To: Y(2)
0 0.02 0.04 0.06 0.08 0.1 0. 0
1
2
3
To: Y(3)
Now we have a maximum speed of .125 m/s, a maximum current draw of approx. 2.25 A and a fast response. Perhaps this motor is larger than needed (note also that this motor is intended to run at 120-170V). So, an SM160A motor is tried with the 24V input voltage; Jarmature = 5e-6 kg m^2 ; kt = .038 N.A; kb=4.0260/(2pi*1000) N m s; L= .53e-3 H, R=3.43 O
Step R es pons e
Tim e (s ec)
Am plitude
0
From : U (1)
To: Y(1)
0
To: Y(2)
(^00) 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.
1
2
3
4
To: Y(3)
Notice that the response time is still acceptable, but the final speed is low and the current draw is high. If a higher motor volatage is tried (24V):
Step R es pons e
Tim e (s ec)
Am plitude
0
From : U (1)
To: Y(1)
0
1
To: Y(2)
(^00) 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.
5
10
To: Y(3)
