





























































































Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
The importance of tray efficiency in batch distillation processes and its effect on model fidelity. It highlights the variation of tray efficiency with tray composition and the need to account for this variation in batch distillation simulations. The document also explores the methods used to estimate tray efficiency and the potential dangers of using constant and equal tray efficiencies for all components.
Typology: Summaries
1 / 238

This page cannot be seen from the preview
Don't miss anything!





























































































Tray Efficiency Effects in Batch Distillation
B.Sc., M.Sc.
This work is dedicated to my parents, Mr Ukeje O. Eloagu Mrs. Florence M. Ukeje-Eloagu And to my siblings Nneoma Ngozi Ihuarulam (Wawam) Onyekachi
SUMMARY
Computer simulation has long been recognised as a useful tool in improved process operation and design studies. Commercial simulation packages now available for batch distillation studies typically assume constant tray efficiency. Here, on the basis of both practical work and computer simulation, the effects of tray efficiency variation with tray liquid composition on model accuracy and column performance are investigated.
Detailed modelling studies were carried out on a pilot batch distillation unit and tray efficiency was found to be an important factor affecting the model fidelity. Distillation of different methanoVwater mixtures revealed that tray efficiency varies with the mixture composition on the tray, the form of the variation being for the efficiency to pass through a minimum at intermediate compositions.
This variation of tray efficiency with tray composition IS a known phenomenon, which has not been included in batch distillation simulations even though tray compositions change significantly during a batch run. The model developed in this work (Variable Efficiency Model) includes the tray efficiency variation with mixture composition and results in an evident improvement in model accuracy for methanoVwater distillation.
The potential effects of strong tray efficiency dependence on mixture composition, at a more general level, are investigated using two case studies, based on hypothetical extensions of the tray efficiency concentration dependence observed for methanoVwater mixtures. In extreme cases, the efficiency-composition dependence could introduce a significant additional non-linearity to the process behaviour, resulting in unexpected composition and temperature movements. To quantify the potential significance of these effects, the economic performance of a column based on simulation using the Variable Efficiency Model was compared with its performance, using an
overall column efficiency (which is the common practice). Using fixed column efficiency was found to under-predict column performance for low purity products and over-predict performance for high purity products.
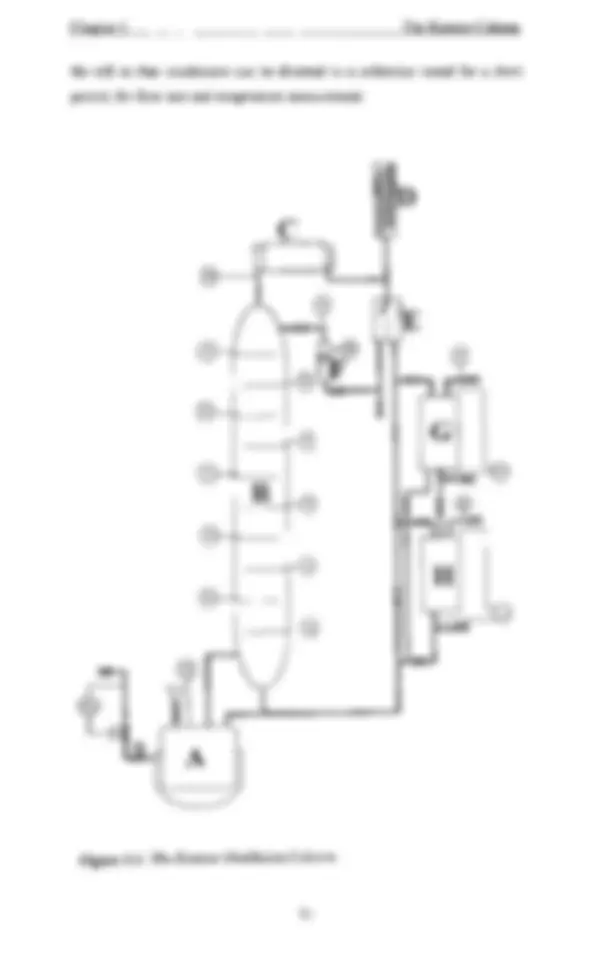
- 2.6.1 Hole Size and Outlet Weir Height - 2.6.2 Reflux Ratio and Tray Holdup - 2.6.3 Fluid Flow Regime - 2.6.4 Liquid Viscosity - 2.6.5 Surface Tension Effects - 2.6.6 Concentration Effects - 2.7 SUMMARY - CHAPTER 3. THE KESTNER COLUMN - 3.1 THE STILL / BOILER - 3.2 THE COLUMN - 3.3 THE CONDENSER - 3.4 EXPE~NTALPROCEDURE - 3.4.1 Sampling Procedure - CHAPTER 4. THE SIMULATION MODEL - 4.1 MODEL SPECIFICATIONS - 4.2 MODEL ASSUMPTIONS - 4.3 MODEL EQUATIONS - 4.3.1 Main Column Equations - 4.3.2 Vapour Liquid Equilibrium - 4.3.3 The Heat Input and Fluid Flow Rates. - 4.3.4 Variable Tray Efficiency LIST OF FIGURES
Figure 2.1: Equilibrium Curve for an Azeotropic Mixture. 9 Figure 2.2: Different Configurations of Batch Distillation Columns (Davidyan et. al. (1994». 13 Figure 2.3: Interfacial Contacting on a Perforated Plate for a Positive and a Negative System (from Ellis & Legg (1962». 43 Figure 3.1: The Kestner Distillation Column. 51 Figure 3.2: Bubble Cap Tray Details. 52 Figure 4.1: Column Section for Arbitrary Trays, n, n-1 and Top of Column. 62 Figure 4. 2: Flowchart of Program Algorithm 69 Figure 5.1: Steady State Temperature and Composition Profiles for Run 1 and Run 2 74 Figure 5.2: Column Steady State Profiles for Run 3 after Initial Total Reflux Startup and after Timed Product Withdrawal. 77 Figure 5.3: Temperature and Composition Movements in the Column during Product Withdrawal for Run 3 78 Figure 5.4: Column Steady State Profiles and Temperature Movements during Product Withdrawal for Run 4. 81 Figure 5.5: Column Steady State Profiles and Temperature Movements during Product Withdrawal for Run 5 83 Figure 5.6: Column Steady State Profiles and Temperature Movements during Product Withdrawal for Run 6 84 Figure 5.7: Column Steady State Profiles and Temperature Movements during Product Withdrawal for Run 7 85 Figure 5.8: Constant Efficiency Model Profiles at Steady State Compared with Profiles from Dribika (1986) for the Drib -1 example 88 Figure 5.9: Constant Efficiency Model Profiles at Steady State Compared with Profiles from Dribika (1986) for the Drib -2 example 89
Figure 5.10: Constant Efficiency Model Profiles at Steady State Compared with Profiles from Dribika (1986) for the Drib- example 90 Figure 5.11: Cyc1ohexane-Toluene Distillation results - Example 1 (Domench et al (1974)). 93 Figure 5.12: Cyc1ohexane-Toluene Distillation results - Example 2 (Domench et al (1974)). 93 Figure 6.1: Tray Efficiency vs. Concentration for Runs 3 to 7. 97 Figure 6.2: Polynomial Best-Fit Curve for Tray Efficiency as a Function of Methano I Concentration Figure 6.3: Constant & Variable Efficiency Model Steady State Temperature and Composition Profiles for Run 3. Figure 6.4: Constant & Variable Efficiency Model Steady State Temperature and Composition Profiles for Run 5 Figure 6.5: Constant & Variable Efficiency Model Steady State Temperature and Composition Profiles for Run 6 Figure 6.6: Constant & Variable Efficiency Model Steady State Temperature and Composition Profiles for Run 7 Figure 6.7: Experimental and Simulation (Variable and Constant Efficiency) Temperature Movements on Trays 2, 3, 4 and 5
between the Initial and Final Steady States for Run 3. 103 Figure 6.8: Experimental and Simulation (Variable and Constant Efficiency) Temperature Movements on Trays 7, 8, 9 and 10 between the Initial and Final Steady States for Run 4. 103 Figure 6.9: Experimental and Simulation (Variable and Constant Efficiency) Temperature Movements on Trays 3, 4, 5 and 6 between the Initial and Final Steady States for Run 5 Figure 6.10: Experimental and Simulation (Variable and Constant Efficiency) Temperature Movements on Trays 3, 4, 5 and 6
between the Initial and Final Steady States for Run 6 104 Figure 6.11: Experimental and Simulation (Variable and Constant Efficiency) Temperature Movements on Trays 3, 4,5 and 6 between the Initial and Final Steady States for Run 7 105
Figure 7.15: Distillate Composition Profiles for Case Study 2 with Distillate Withdrawal Start Time, t=2.0 hrs at Reflux Ratio of 4.5. 134 Figure 7.16: Composition Trajectory on All Trays during Product Withdrawal until all Methanol is Distilled for Efficiency Curve E2.0q. 134 Figure 7.17: Case Study 2 Distillate Composition & Reflux Ratio Profiles For 92% MeOH Product - Fixed Distillate Composition Operation 136 Figure 7.18: Case Study 2 Distillate Composition & Reflux Ratio Profiles For 99% MeOH Product - Fixed Distillate Composition Operation (^136) Figure 7.19: Product and Steam Utilities for Simulation Using the Different Efficiency Curves for a 92% Methanol Specification 143 Figure 7.20: Product and Steam Utilities for Simulation Using the Different Efficiency Curves for a 99% Methanol Specification 144 Figure 7.21: Annual Performance of the Different Efficiency Curves for a 92% and a 99% Methanol Specification. 145 Figure A.1: Steam and Vapour Boilup Rates for the Column Using Water as a Test Fluid. 183 Figure A.2: Experimental and Simulation Steady State Temperature and Composition Profiles for Runs T2 and T3 187 Figure B.1: Main Program Listing. 193 Figure B.2: Bubble Point Temperature Subroutine Listing. 197 Figure B.3: Subroutine INITIAL Listing for Column Data Initialisation 199 Figure B.4: Subroutine HOLDUP Listing. 202 Figure B.5: Subroutine REBOIL, Fluid rates and Reflux Ratio Calculation Listing. Figure B.6: Subroutine ENTH, Enthalpy Calculations Listing.
Figure B.7: Subroutine DERIV Listing 204 Figure B.8: Subroutine Euler Numerical Integration Program Listing. 205 Figure B.9: Subroutine DYNEFF Listing. 207 Figure B.1 0: Subroutine DRA WDIST Listing. 208 Figure B.11: Subroutine PRES Listing for Output of Simulation Results. 211
Figure B.12: Subroutine PDRG Listing, for Output of Composition Results 212 Figure B.13: Subroutine HEADER Listing for Writing Output File Headers 213
Table A.2: Feed and Operating Conditions and Results of Experimental Runs and Equivalent Simulation Runs. Table B. 1: Sample Data File for the Simulation Table B. 2: Sample Output File TI-3.ANS Table B. 3: Sample Output File Tl-3.DRG
Table C.1: Table of Antoine Constants (Coulson and Richardson (I993)) 221 Table C.2: Physical Properties of the Mixture Components 221 Table C.3: Wilson Coefficients, Aij for Methanol-Water System (Hirata et al (I975)) 222 Table C.4: Wilson Coefficients, Aij for Methanol-Ethanol-Propanol System (Hirata et al (I 975)) 222 Table C.5: Wilson Coefficients, Aij for Cyclohexane-Toluene System (Hirata et al (1975)) 222
CHAPTER ONE.
INTRODUCTION
In the chemical process industry, various processing units such as chemical reactors, evaporators, distillation columns, phase separators, extractors, heat exchangers, etc. or a combination of these units are used to transform raw materials and energy into finished products. This is done discretely, continuously or batchwise.
Discrete processes are generally used in the manufacture of consumer goods (e.g. cars, computers, furniture, etc) while continuous processes are more widely used in the bulk chemical and petrochemical process industries. Batch processing on the other hand, finds more widespread use in pharmaceutical, dyestuff, specialty chemicals and agrochemical industries. Compared with continuous processes, batch processes have attracted relatively little attention from the academic world, and have not been associated with large investments in industrial process technology research despite its immense contribution to wealth creation (Sharratt (1997)). Currently however, the spread of continuous processing for bulk chemicals production appears to be in reverse in the developed world. This point is highlighted by Freshwater (1994) who points out that while profitability in petrochemicals (a continuous process sector) fell by 25% in 1992, pharmaceuticals was the fastest growing area with an increase of 20% in the same year.
Continuous and batch processes (including distillation) offer a number of contrasts, reflected in the technical and economic factors, which govern the choice between them. One major advantage of continuous processing is economy of scale (Sawyer (1993)). High volume production of a standard product generally yields a good return on the initial capital investment and if product requirements do not change significantly, the process will require a
1
Chapter 1 (^) Introduction
The outlook on bulk chemicals (continuous process) production is changing as a result of falling profit margins, changing markets and strong competition from emerging nations, often with cheaper raw materials and labour costs. The technological advantages available to chemical companies in developed nations no longer overcome the lower wage costs, growing markets and desire for new industry in the developing nations. Such threats to profitability have led major companies to try to move back into the specialty and fine chemicals sector where products have higher added value, for larger profit margins.
In the fine chemicals industry for instance, recent estimates of annual worldwide production are in the range US $26-64 billion, with the world market for fine chemicals in 1995 estimated at US $42 billion (Sharratt (1997)). Of this, 30% was used as pharmaceutical intermediates, 35% for pesticides, 23% for flavours and fragrances and 12% for other uses. Growth is expected mainly in the pharmaceutical sector at 6% annually, with pesticides growing at about 1 %, and the average growth in the production of fine chemicals continuing at about 5% (Sharratt (1997)).
In these process and chemicals industries, separation is a vital unit operation used for waste treatment, product concentration, etc. Numerous novel separation methods and techniques have been developed to date but distillation, which is one of the oldest methods, still remains the most important and widely used separation method.
Distillation columns constitute a significant fraction of the capital investment in chemical plants and refineries around the world. The operating costs of these columns often constitute a major proportion of the total operating cost of many processes e.g. distillation columns consume some 95% of the total energy used in separation and this amounts to roughly 3% of the total energy consumed in the United States alone (Ognisty (1995)). It is becoming of great economic importance to run a distillation column as optimally as possible.
3
Chapter 1 (^) Introduction
The aggressive nature of the market and strong competition makes it essential to reduce lead times between decision to invest and first production since the first product to corner a market is usually the most successful. One useful technique in reducing this lead-time (at the process design stage), which has also found wide applicability in control and operation studies, is dynamic simulation. This involves the construction of a mathematical model, based on time-dependent differential equations that represent the changes in a process with time.
Early models, for example distillation models, include the McCabe-Thiele steady state model, which is restricted to binary distillation. The level of detail in this and other early models was very much constrained by the rigours of the computations involved and was thus greatly simplified. Advances in computer power and in modelling methods have rendered obsolete many of the simplifications and special modifications which were necessary in earlier models. Until recently however, much of the development in computer simulation has been in the area of steady state, continuous process simulators, with batch, dynamic simulation receiving very little attention in comparison.
Computer models permit the handling of greater degrees of complexity in the design and analysis of the operation of batch separation. Commercial simulation packages exist for the modelling of batch process plants or process units, including distillation. These models can be used to augment or replace experimental studies, depending on the complexity and accuracy of the model used. The effort and investment devoted to producing exact models must be balanced by the benefits realised from its use.
Recent focus in batch processes has been directed at improved simulation techniques and the automation of aspects of batch processing by use of expert systems. Most of the techniques used attempt to transfer the philosophies and methodologies of continuous processing for use in batch processing without full consideration of the realm and constraints under which batch processes operate. 4